ST_ClosestPoint#
Table of Contents#
Part 1: What is ST_ClosestPoint?#
Part 1.1: Overview#
ST_ClosestPoint is similar to ST_Snap. Given a point and another geometry, it finds the closest point on the geometry. ST_ClosestPoint will always return the same snap point that ST_Snap will for point to polyline cases.
ST_ClosestPoint and ST_Snap differ on the point to polygon case when the point is contained in the polygon:
ST_ClosestPoint will return the snap point as the same input point if the point is contained in the polygon.
ST_Snap will return the snap point as the closest point on the polygon border if the point is contained in the polygon.
In addition, ST_ClosestPoint will return additional attributes along with the snap location (that ST_Snap will not):
SHAPE: The snap location as a point geometry.distance: The distance between the input point and snap location on the geometry.index: The index of the vertex in the geometry that the point was snapped to.rightside: A boolean indicating if the point was snapped to the right side of the geometry.
The below image shows how the red point on the right snaps to the blue geometry. The transparent, dotted red point on the left represents the snap location.
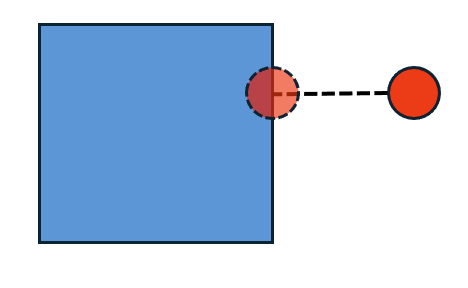
Part 1.2: Index Attribute Explained#
The behavior of the index attribute is as follows. Each of the cases are outlined and visualized below. The input point is in red and the geometry is in blue. The dotted line represents the line to the snap location. The chosen vertex index is in bold.
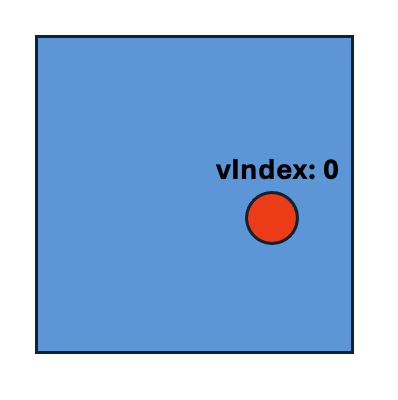
Case 1: Point to Polygon. Point is contained in the polygon: The vertex index is 0.
In this case, because the point is contained in the polygon, the output snap point is identical to the input point and the index is 0.
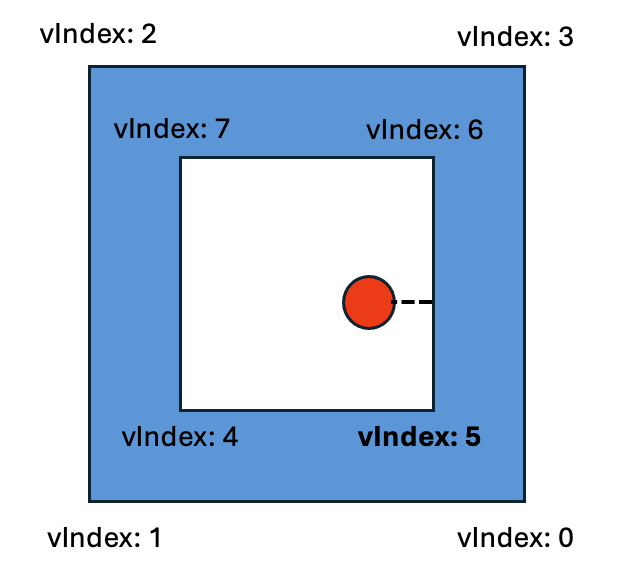
Case 2: Point to Polygon. Point is not contained in the polygon: The vertex index is the start vertex index of a segment with the closest coordinate.
In this case, the point is not contained in the polygon. The output snap point is the point on the segment with the closest snap coordinate. In the example below, the segment with the closest snap coordinate is the segment starting at vertex 5 and ending at vertex 6. Therefore, vertex 5 is the vertex index.
Note: Outer rings of a polygon are always drawn clockwise, and inner rings are always drawn counter-clockwise.
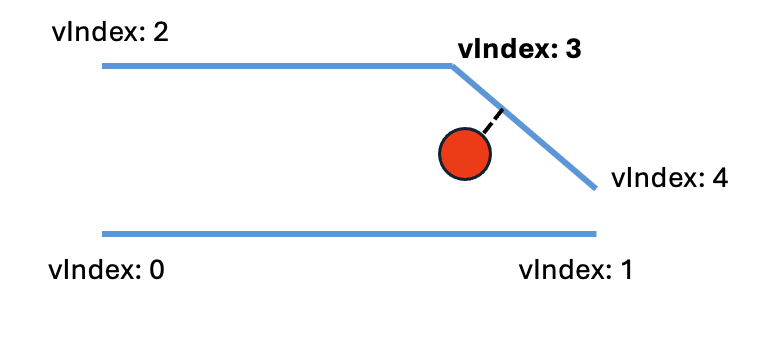
Case 3: Point to Polyline: The vertex index is the start vertex index of a segment with the closest coordinate.
In this case, the output snap point is the point on the segment with the closest snap coordinate. In the example below, the segment with the closest snap coordinate is the segment starting at vertex 3 and ending at vertex 4. Therefore, vertex 3 is the vertex index.
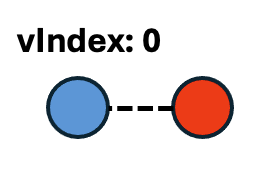
Case 4: Point to Point: The vertex index is 0.
In this case, the output snap point is just the other input point because there are no other options. Therefore, the vertex index is 0.
In the point to point case, it is always true that the first point will be the snap location (blue) and the second point will be the point to snap (red).
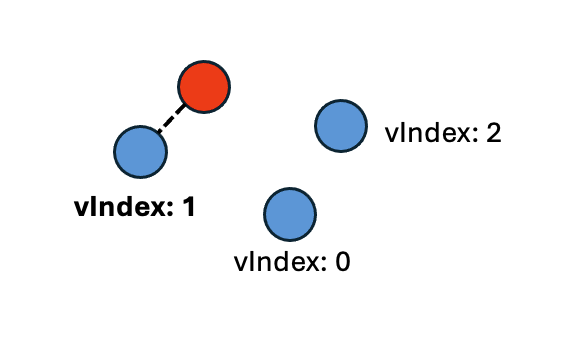
Case 5: Point to Multpoint: The vertex index is the closest vertex.
In this case, the output snap point is the closest point in the multipoint. In the example below, the closest point in the multipoint is the point with vertex 1. Therefore, the vertex index is 1.
Case 6: Input is invalid or not a supported type: The vertex index is -1.
Part 1.3: Rightside Attribute Explained#
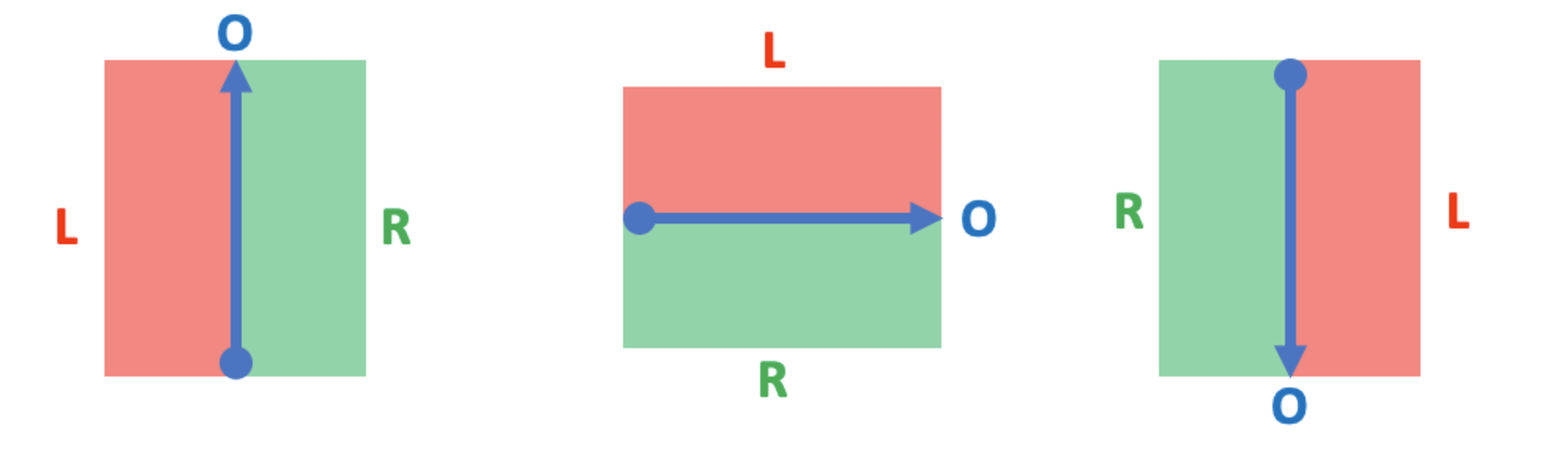
The
rightsideattribute indicates the side of the segment the point was snapped to. The possible values aretruemeaning right side, andfalsemeaning left side. The below image shows which side is which relative to a line segment drawn in different directions.If the point is directly on the line segment, then it is considered to be on the right of the line.
The side is calculated by taking the cross product of the following vectors:
\(\mathbf{p} - \mathbf{a} \quad \text{(vector from a to p)}\)
\(\mathbf{b} - \mathbf{a} \quad \text{(vector from a to b)}\).
In the image above, a is the blue start point and b is the blue end arrow. Point p is not shown.
The final formula is:
\((\mathbf{p} - \mathbf{a}) \times (\mathbf{b} - \mathbf{a})\)
Left or right is determined by checking the sign of the cross product (negative or positive).
Part 2: Using ST_ClosestPoint#
[ ]:
import bdt
import math
bdt.auth("bdt.lic")
from bdt import functions as B
from pyspark.sql.functions import col, inline, array
BDT has been successfully authorized!
Welcome to
___ _ ___ __ ______ __ __ _ __
/ _ ) (_) ___ _ / _ \ ___ _ / /_ ___ _ /_ __/ ___ ___ / / / /__ (_) / /_
/ _ | / / / _ `/ / // // _ `// __// _ `/ / / / _ \/ _ \ / / / '_/ / / / __/
/____/ /_/ \_, / /____/ \_,_/ \__/ \_,_/ /_/ \___/\___//_/ /_/\_\ /_/ \__/
/___/
BDT python version: v3.5.0-v3.5.0
BDT jar version: v3.5.0-v3.5.0
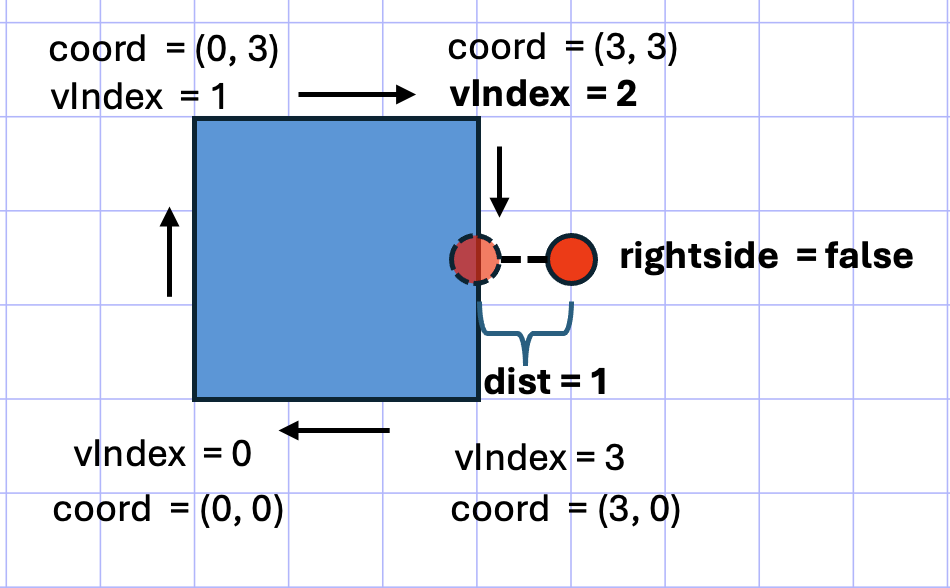
Below is an image of the example that will be run. The image includes both the input geometries and the expected output values.
Notice that
rightside = false. This is due to the drawing order of the polygon. The arrows represent the drawing order.
[ ]:
point_wkt = "POINT (4 1.5)"
poly_wkt = "POLYGON ((0 0, 3 0, 3 3, 0 3, 0 0))"
df = spark.sql(f"""
SELECT
ST_FromText('{point_wkt}') AS POINT,
ST_FromText('{poly_wkt}') AS POLYGON
""")
df.show()
+--------------------+--------------------+
| POINT| POLYGON|
+--------------------+--------------------+
|{[01 01 00 00 00 ...|{[01 06 00 00 00 ...|
+--------------------+--------------------+
[ ]:
result_df = (df.select(
inline(
array(
B.st_closest_point("POINT", "POLYGON")
)
)
))
result_df.show(truncate=False)
+--------------------------------------------------------------------------------------+--------+-----+---------+
|SHAPE |distance|index|rightside|
+--------------------------------------------------------------------------------------+--------+-----+---------+
|{[01 01 00 00 00 00 00 00 00 00 00 08 40 00 00 00 00 00 00 F8 3F], 3.0, 1.5, 3.0, 1.5}|1.0 |2 |false |
+--------------------------------------------------------------------------------------+--------+-----+---------+